Beräkna tangentplanet till grafen till funktionen \(f(x,y)=x^2-y^2\) i punkten \((1,2,-3)\).

Planet kan dels skrivas på ekvationsform som \[2x-4y-z=-3\]. Planets parameterform blir \[ \left[\begin{array}{c}x \\y \\z\end{array}\right]= \left[\begin{array}{c}1 \\0 \\2\end{array}\right]s+ \left[\begin{array}{c}0 \\1 \\-4\end{array}\right]t+\left[\begin{array}{c}1 \\2 \\-3\end{array}\right] \]

Nyckeln till lösningen av uppgiften ligger i att grafen till en funktion dels lätt kan skrivas som en nivåyta och dels har en väldigt rättfram parametrisering. Grafen till vår funktion är nivåytan \(g=0\) för funktionen \[ g(x,y,z)=x^2-y^2-z \] Denna funktions gradient i vår punkt blir \[ \nabla g|_{(1,2-3)}=(2x,-2y,-1)|_{(1,2-3)}=(2,-4,-1) \] Enligt vad vi lärde oss i Räkneövning 4 så har vi att denna gradientvektor är tangentplanets normalvektor och då ges tangentplanet av ekvationen \[ (2,-4,-1)\bullet (x-1,y-2,z+3)=0\quad \] som ger oss \[ 2x-4y-z=-3 \] Detta är tangentplanets ekvation.
Om vi vill skriva tangentplanet på parameterform så kan vi enligt räkneövning 4 använda partialderivatorna till funktionsgrafens parametrisering men innan vi kan göra det så behöver vi beräkna en sådan parametrisering av funktionsgrafen. Detta är ganska enkelt i vårt fall: sätt \(x=u\) och \(y=v\) och \(z=f(x,y)=f(u,v)=u^2-v^2\): \[ S(u,v)=(u,v,f(u,v))=(u,v,u^2-v^2) \] Partialderivatorna blir därför \[ \begin{split} \frac{\partial S}{\partial u}\Bigg|_{(1,2)}&=\left[\begin{array}{c}1 \\0 \\2u\end{array}\right]_{(1,2)}=\left[\begin{array}{c}1 \\0 \\2\end{array}\right] \\ \frac{\partial S}{\partial v}\Bigg|_{(1,2)}&=\left[\begin{array}{c}0 \\1 \\-2v\end{array}\right]_{(1,2)} =\left[\begin{array}{c}0 \\1 \\-4\end{array}\right] \end{split} \] Detta ger oss att tangenplanet genom vår punkt blir \[ \left[\begin{array}{c}x \\y \\z\end{array}\right]= \left[\begin{array}{c}1 \\0 \\2\end{array}\right]s+ \left[\begin{array}{c}0 \\1 \\-4\end{array}\right]t+\left[\begin{array}{c}1 \\2 \\-3\end{array}\right] \]

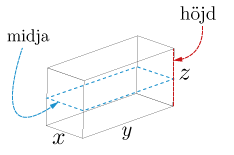
Ett postföretag levererar bara paket i form av rektangulära lådor med midja och höjd uppfyller vissa villkor. Midjan är omkretsen av ett horisontellt tvärsnitt. (Se figur nedan) Vilkoret som paketet måste uppfylla är att summan av midjan och paketets höjd får vara högst 120 cm. Beräkna den största volym som en sådan låda kan ha.

\(x=y=20\)cm, \(z=40\) cm. Volymen blir 16000 \(cm^3\) eller 16 liter.

Vi har den rektangulära lådans sidor givna som \(x\), \(y\) och \(z\). Vår uppgift är att maximera volymen \(V(x,y,z)=x\cdot y\cdot z\) under bivillkoret att \[ \underbrace{2x+2y}_{=\text{ midjan }}+z=120 \] Vi ställer därför upp Lagrangefunktionen: \[ L(x,y,z,\lambda)=xyz-\lambda(2x+2y+z-120). \] Nu söker vi kritiska punkter till Lagrangfunktionen, vilket kräver att vi hittar värden på variablerna som gör att Lagrangefunktionens partialderivator blir noll: \begin{eqnarray*} \frac{\partial L}{\partial x} & = & yz-2\lambda=0 \quad\Rightarrow\quad 2\lambda =yz \\ \frac{\partial L}{\partial y} & = & xz-2\lambda=0\quad\Rightarrow\quad 2\lambda= xz\\ \frac{\partial L}{\partial z} & = & xy-\lambda =0\quad\Rightarrow\quad 2\lambda= 2xy\\ \frac{\partial L}{\partial \lambda} & = & -2x-2y-z+120=0 \end{eqnarray*} De tre första ekvationerna av detta system ger att \(z=2x=2y\) som insatt i bivillkorekvationen (den fjärde partialderivatan till Lagrange) blir \(3z=120\). Vi får att \(x=20\), \(y=20\) och \(z=40\) och den maximala volymen blir således \[ V=20\cdot 20\cdot 40=16\ 000 \ cm^3 \] Uttrycker man sidorna i dm så har vi volymen \[ 2\cdot 2\cdot 4= 16 \ dm^3= 16 \text{ liter} \]

Hitta och klassificera alla kritiska punkter till funktionen \(f(x,y)=x^2y(2-x-y)\)

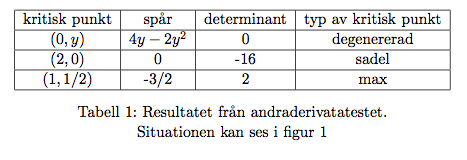
Om \(x=0\) så har vi, för alla \(y\), en obestämbar (degenererad) kritiska punkt (en hel linje). Dessa är maxima om \(y<0\) och om \(y>2\). Minima om \( y\in (0,2) \) och sadelpunkter om \(y=0\) och om \(y=2\). \((2,0)\) är en sadelpunkt och \((1,1/2)\) är ett maximum.

Vi beräknar derivatorna: \[ \begin{split} \frac{\partial f}{\partial x} &=-x y (3 x+2 y-4)\\ \frac{\partial f}{\partial y} &=-x^2 (x+2 y-2) \end{split} \] Vi får att \( (0,y)\) är kritisk punkt för alla värden på \(y\). Om \(y=0\) så får vi \(x=2\) från faktorn \(x+2y-2\) så \((2,0)\) är kritisk punkt. För \(x\neq 0\neq y\) så gäller att båda faktorerna \(3x+2y-4\) och \(x+2y-2\) måste vara noll vilket leder tillpunkten \((1,1/2)\) är en kritisk punkt. Vi klassificerar punkterna med hjälp av andraderivatatestet. Låt oss börja med att beräkna andraderivatorna \[ \begin{split} \frac{\partial^2 f}{\partial x^2} &=-2 y (3 x+y-2)\\ \frac{\partial^2 f}{\partial y^2} &=-2 x^2\\ \frac{\partial^2 f}{\partial x\partial y} &=-x (3 x+4 y-4) \end{split} \] Vi sammanställer resultatet från andraderivatatestet i följande tabell.: 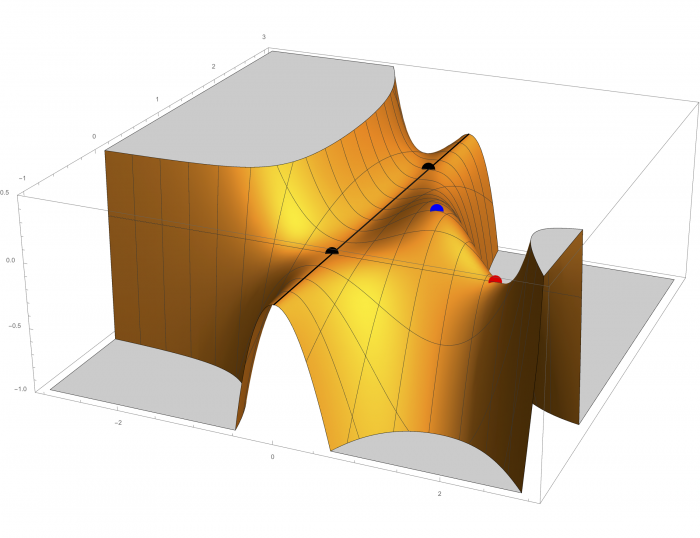Kritiska punkterna \((0,y)\) ligger på den svarta linjen och vi har att funktionen är konstant på denna linje. Detta gör att vi på den svarta linjen inte har strikta max, min eller sadelpunkter. Tittar man noggrant så ser vi att för varje fixt \(y\) så är andra derivatan map \(x\) lika med \(2y(2-y)\) och denna derivata är positiv om \(02\). För varje fixt \(y\) så ger andraderivatatestet i en variabel så ger detta att vi har minimum där derivatan är positiv och max där derivatan är negativ. Men max och min i detta fall är inte helt strikt eftersom funktionen är konstant längs linjen \((0,y)\). Det är detta som degenererad betyder i detta fall. Kritiska punkterna är minima mellan de två svarta punkterna. Utanför har vi maxima. I de svarta gränspunkterna \((0,0)\) och \((0,2)\) har vi sadelstruktur eftersom funktionens värden ökar i vissa riktningar och avtar i andra. Den röda punkten är \((2,0,0)\) (sadel) och den blå är \((1,1/2,1/4)\) (max).}