Denna föreläsning introducerar parameterkurvor, visar hur man beräknar dessa kurvors längd och hur man beräknar kurvintegraler.
Lecture 11 :: Parameterkurvor och kurvintegraler
11
Lecture :: parmeterkurvor och kurvintegraler.
sammanfattning
Läsanvisningar::
- Avsnitt i kursboken
- Detta material svarar mot Adams Kapitel 11.1, 11.3 samt 15.3
- Rekommenderade uppgifter om
kurvor -
11.1 :: 1, 5, 7, 9, 11, 15
11.2 :: 1, 5, 7, 9, 13, 15, 17
Definition av Parametriska kurvor.
Parametriska kurvor
En Parametrisk kurva i \(\mathbb{R}^n\) är en funktion
\[
r(t)=(x_1(t),\dots,x_n(t))
\]
En tolkning av denna funktion är att den anger en partikels position i rummet
som funktion av tiden. När tiden varieras så anger funktionen partikelns bana i rummet.
Partikelns hastighet är funktionens derivata:
\[
v(t)=\frac{dr}{dt}=(x_1'(t),\dots,x_n'(t))
\]
Partikelns accelleration är hastighetens förändring och ges alltså som tidsderivatan av hastigheten
och vi får
\[
a(t)=v'(t)=r''(t)=(x_1''(t),\dots, x_n''(t))
\]
Övning 1::
En partikel rör sig i en cirkulär bana med parametriseringen
\[
r(t)=(5\cos t, 5\sin t)
\]
Beräkna partikelns position, hastighet och accelleration då \(t=\pi/2\)
Lösning ::
Positionen är \[r(\pi/2)=(0,5)\]
Hastigheten blir \[ v(t)=(-5\sin t,5\cos t)|_{\pi/2}=(-5,0) \] och accellerationen blir \[ a(t)=(-5\cos t,-5\sin t)|_{\pi/2}=(0,-5) \]
Hastigheten blir \[ v(t)=(-5\sin t,5\cos t)|_{\pi/2}=(-5,0) \] och accellerationen blir \[ a(t)=(-5\cos t,-5\sin t)|_{\pi/2}=(0,-5) \]
Video :: Introduktion till parameterkurvor
Grafen som parameterkurva
Exempel ::
Grafen till en funktion \(y=f(x)\) av en variabel tänker vi ofta som en kurva i planet. Denna grafkurva kan vi också tolka som en parameterkurva genom parametriseringen \[ r(t)=(t,f(t)) \]
Grafen till en funktion \(y=f(x)\) av en variabel tänker vi ofta som en kurva i planet. Denna grafkurva kan vi också tolka som en parameterkurva genom parametriseringen \[ r(t)=(t,f(t)) \]
Övning 2::
Beräkna en parematrisering av grafen till \(f(x)=\sin x\)
Lösning ::
Grafens parametrisering blir
\[
r(t)=(t,\sin t)
\]
Video ::Exempel på parameterkurvor
Längden av kurvor
Exempel 1::
Längden av en kurvsegment \(C\) med parametriseringen \(r(t)\) ges av \[ \int_C ds =\int_a^b ||r'(t)||dt, \] där \(a\) och \(b\) är segmentets ändpunkter map parametern \(t\).
Längden av en kurvsegment \(C\) med parametriseringen \(r(t)\) ges av \[ \int_C ds =\int_a^b ||r'(t)||dt, \] där \(a\) och \(b\) är segmentets ändpunkter map parametern \(t\).
Övning 4::
Beräkna längden av grafen till funktionen \(y = \frac{x^2}{2}\) från \(0\) till \(1\).
Lösning ::
Parametriseringen av grafen ges av \(r(t)=(t,\frac{t^2}{2})\). Vi får att \(r'(t)=(1,t)\), \(||r'[t]||=\sqrt{1+t^2}\), och
längden blir därför
\[
\begin{split}
\int_0^1 \sqrt{1+t^2} dt &=\text{ knepig integral }=\\
&=\left[\frac{t}{2}\sqrt{1+t^2}+\frac{1}{2}\ln(t+\sqrt{1+t^2})\right]_0^1=\\
&=\frac{1}{\sqrt{2}}+\frac{1}{2}\ln [ 1+\sqrt{2} ]
\end{split}
\]
Den knepiga integralen löste jag mha formelsamling (t.ex. Adams Bakre Pärminsida).
Jag har upptäckt att denna integral dyker upp på några ställen, t.ex. i en av de rekommenderade
uppgifterna i kapitel 15. Jag har därför gjort en räkneövning (RÖ 19) som härleder denna formel, även om
detta, strikt sett, är ett problem från envariabelanalysen.
Video :: Längden av en kurva
Längden av cirkeln
Övning 5::
Beräkna längden av en cirkel. Härled alltså formeln för cirkelns omkrets genom
att integrera över ett varv på cirkeln med den vanliga parametriseringen.
Lösning ::
Cirkeln med radien \(r\) har parametriseringen
\[
c(t)=( r\cos t, r\sin t)
\]
Vi får att \(||c'(t)||=r\) och därför blir längdintegralen
\[
\int_0^{2\pi} r\cdot dt = \left[ r\cdot t\right]_0^{2\pi}=2\pi r
\]
Video :: Längden av cirkeln
Längden av en Helixkurva
Övning 6::
Beräkna längden av ett varv av helixkurvan med parametriseringen
\[
H(t)=(a\cos t, a\sin t, b\cdot t)
\]
Lösning ::
Vi har att
\[
\begin{split}
||H'(t)|| &=||(-a\sin t, a\cos t, b)||=\\
&= \sqrt{a^2(\sin^2 t+\cos^2 t) +b^2}=\\
&=\sqrt{a^2+b^2}
\end{split}
\]
Detta ger att längdintegralen blir
\[
\int_H ds=\int_0^{2\pi} \sqrt{a^2+b^2} dt =\left[ \sqrt{a^2+b^2}\cdot t\right]_0^{2\pi} =2\pi\sqrt{a^2+b^2}
\]
Video :: Längden av en helixkkurva
Längden av en ellips :: detta är knepigt.
Exempel ::
Här är ett exempel på att längdberäkningar kan bli mycket krångliga och att detta är en del av naturen.
Här är ett exempel på att längdberäkningar kan bli mycket krångliga och att detta är en del av naturen.
Övning 7::
Beräkna längden av ellipsen \[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\]
Lösning ::
Man behöver först hitta en parametrisering. Om man utgår från parametriseringen av en cirkel så kan
vi göra en modifiering som ger oss en parametrisering \(E(t)=(x(t),y(t))\) av ellipsen:
\[
\begin{split}
x &=a\cos t\\
y &=b\sin t
\end{split}
\]
Vi får att
\[
\begin{split}
||E'(t)|| &=\sqrt{a^2\sin^2 t+ b^2\cos^2 t}=\sqrt{ a^2\sin^2 t+b^2(1-\sin^2)}=\\
&=\sqrt{b^2+(a^2-b^2)\sin^2 t}=
b\sqrt{1-\left[\underbrace{\frac{b^2-a^2}{b^2}}_{=K^2}\right]\sin^2 t}=\\
&=b\sqrt{1-K^2\sin^2 t}
\end{split}
\]
Detta ger därför att längden beräknas enligt
\[
b\int_0^{2\pi} \sqrt{1-K^2\sin^2 t}=\text{ elliptisk integral "of the second kind" }
\]
som är en integral som inte kan uttryckas med elementära funktioner.
Läs mer om elliptiska integraler här
Läs mer om elliptiska integraler här
Video :: Längden av en ellips är svår att beräkna.
Kurvintegraler
Kurvintegraler
Integralen \[ \int_C f ds=\int_a^b f(r(t))||r'(t)|| dt \] över kurvan \(C\) med parametrisering \(r(t)\) kallas för en kurvintegral.
Om \(f\) tolkas som en höjd ovanför kurvan så kan vi tolka kurvintegralen som att vi räknar ut arean av ett staket. Se bild.
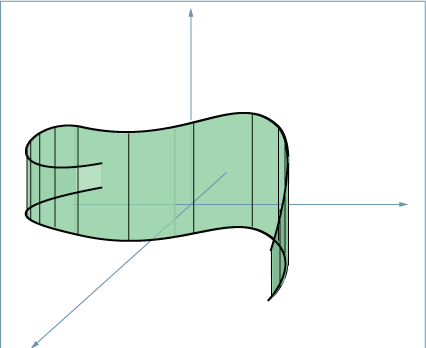
Integralen \[ \int_C f ds=\int_a^b f(r(t))||r'(t)|| dt \] över kurvan \(C\) med parametrisering \(r(t)\) kallas för en kurvintegral.
Om \(f\) tolkas som en höjd ovanför kurvan så kan vi tolka kurvintegralen som att vi räknar ut arean av ett staket. Se bild.

Video :: Introduktion till kurvintegraler
Beräkning av kurvintegral
Övning 8::
Beräkna arean av den den del av cylindern \(x^2+y^2=1\) som
ligger ovanför \(z=0\) men under planet \(y=z\)
Lösning ::
Vi har en cirkelbåge \(c(t)=(\cos t, \sin t)\), \(0\leq t\leq \pi\).
Höjden bestäms tydligen av \(y\) och arean kan då beräknas med
integralen
\[
\int_0^\pi y\ ds= \int_0^\pi \sin t \ dt=-\cos t|_0^\pi =2
\]
där vi noterar att \(y\) på kurvan heter \(\sin t\) tack vare vår parametrisering.
Video :: Exempel på kurvintegral.